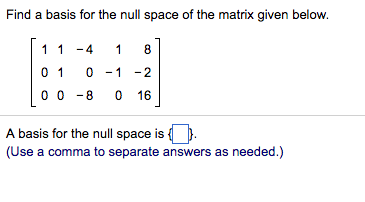
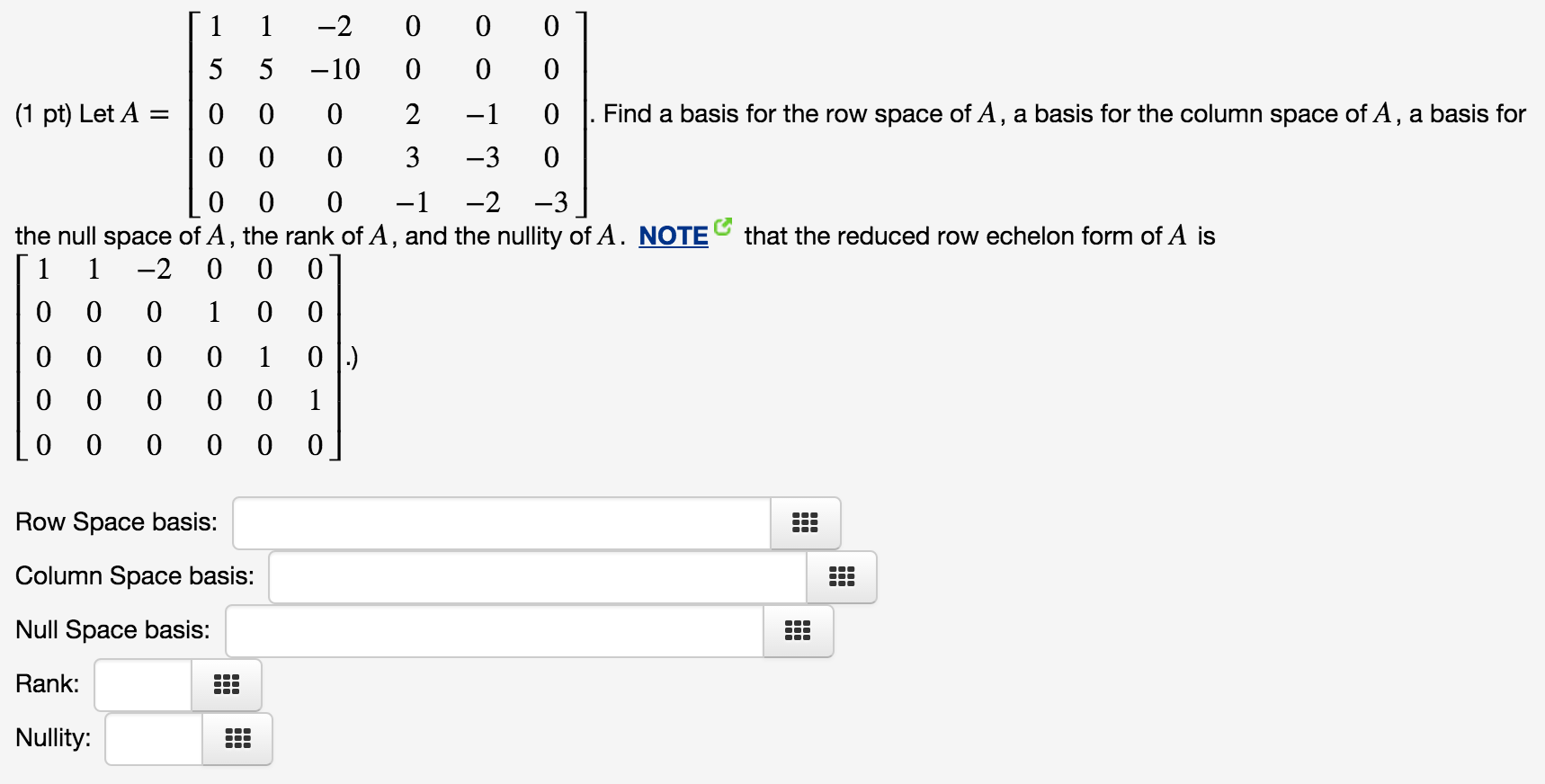
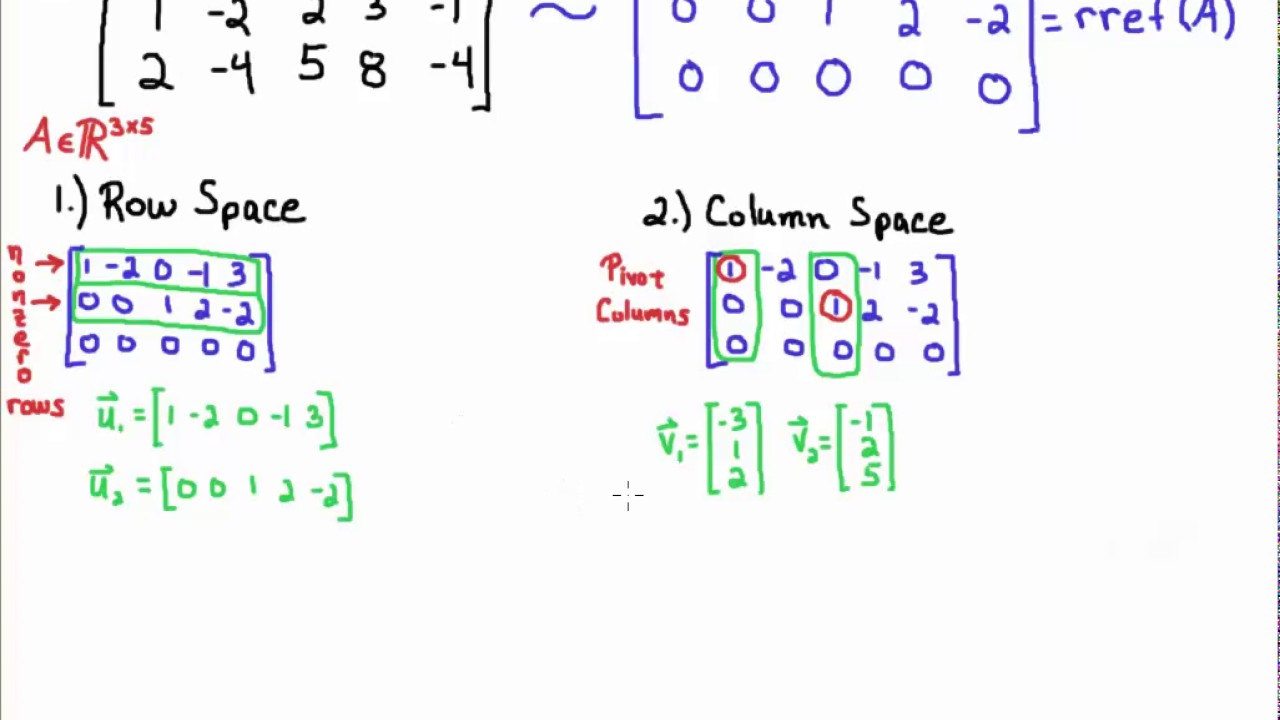
Find Basis For Null Space

E 3x is e 3 x and e 3x is e 3 x. 1 x 2 ln x is 1 x 2 ln x and 1 x 2 ln x is 1 x 2 ln x. A find a matrix b in reduced row echelon form such that b is row equivalent to the matrix a.

desks for small spaces with storage double spaced paragraph double space desks for small spaces ikea destination deep space doctor who space and time double spaced paragraphs dining room tables for small spaces

Solved Find A Basis For The Null Space Of The Matrix Give Chegg Com

Find The Null Space Of A Matrix Youtube

Linear Algebra Example Problems Matrix Null Space Basis And Dimension Youtube

Basis Of A Null Space Of A Matrix Mathematics Stack Exchange

Linear Algebra Example Problems Null Space Example 2 Youtube

Solved Find Bases For The Null Space And Column Space Of Chegg Com

The calculator will find the null space of the given matrix with steps shown.

Find basis for null space. For each free variable set it to 1 and the rest of the free variables to zero and solve for the pivot variables. Notice that the basis vectors do not have much in common with the rows of. In general if a is in rref then a basis for the nullspace of a can be built up by doing the following. Find a basis of the null space of the given m x n matrix a.

Next circle the first non zero entries in each row. The resulting solution will give a vector to be included in the basis. De nition 342 the null space of an m n matrix a denoted null a is the set of all solutions to the homogeneous equation ax 0. Finding a basis of the null space of a matrix.

A 1 1 2 2 2 4 2 3 5. And we already know that the null space of a is equal to the null space of the reduced row echelon form of a. Null space calculator mathdetail mathdetail. Also be careful when you write fractions.

In particular the elements of null a are vectors in rnif we are working with an m n matrix. To find out the basis of the null space of a we follow the following steps. 1 2 3 4 5 6 7 8 9 10 11 12. The number of elements in the basis of the null space is important and is called the nullity of a.

First convert the given matrix into row echelon form say u. Please select the size of the matrix from the popup menus then click on the submit button. In general you can skip parentheses but be very careful. So if this is the reduce row echelon form of a let s figure out its null space.

This null space is said to have dimension 3 for there are three basis vectors in this set and is a subset of displaystyle mathbb r 5 for the number of entries in each vector. That is the dimension of the nullspace of t is n 1. The null space calculator will find a basis for the null space of a matrix for you and show all steps in the process along the way. B let b v 1 v n 1 be a basis of the row equivalent matrix bases for the null space range and row space of a matrix let.

X 2rnand ax 0g remark 343 as noted earlier this is a subspace of rn. 1 2 3 4. Written in set notation we have null a fx. In general you can skip the multiplication sign so 5 x is equivalent to 5 x.

So the null space is the set of all of vectors in r4 because we have 4 columns here.