Basis For Column Space

Thus basis for col a r 2 r 1 r 2 r 3 2r 1 r 3.

Basis for column space. In linear algebra the column space of a matrix a is the span of its column vectors. Null space calculator. Let f displaystyle mathbb f be a field. Calculate a basis for the column space of a matrix step 1.

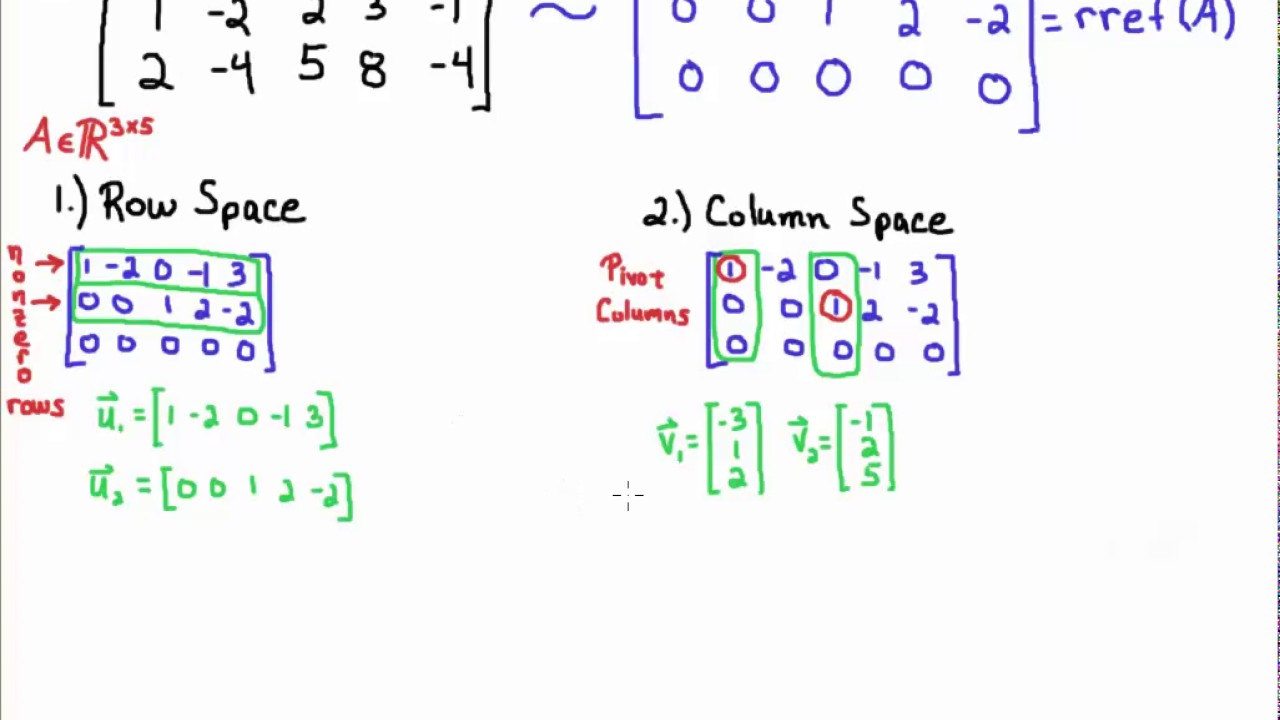
Since the column space of a consists precisely of those vectors b such that a x b is a solvable system one way to determine a basis for cs a would be to first find the space of all vectors b such that a x b is consistent then constructing a basis for this space. Obtained from the columns of a are called the column vectors of a. The dimension of the column space is called the rank of the matrix and is at most min. The subspace of rm spanned by the column vectors of a is called the column space of a.

Find a basis for the nullspace row space and the range of a respectively. A column space of a has associated with it a basis it s not a basis itself it might be if the null space contains only the zero vector but that s for a later video. A definition for. It s a property that it possesses.

A basis for the column space. Now we show how to find bases for the column space of a matrix and the null space of a matrix. We now turn to the main de nitions of this section. The column space calculator will find a basis for the column space of a matrix for you and show all steps in the process along the way.

A basis for col a consists of the 3 pivot columns from the original matrix a. The column space of a matrix is the image or range of the corresponding matrix transformation. Determine the column space of a put a into echelon form. See this important note in section 2 6.

To begin select the number of rows and columns in your matrix and press the create matrix button. The subspace of rn spanned by the row vectors of a is called the row space of a. In order to find a basis for a given subspace it is usually best to rewrite the subspace as a column space or a null space first.